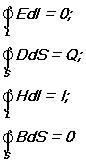Объяснение и создание математической модели физического процесса или явления далеко не всегда можно решить «в лоб». Зачастую, приходиться вводить к основным понятиям некоторые дополнительные аргументы, чтобы показать функцию во всей красе.

Один из ярких примеров такого подхода может служить введение Максвеллом понятия тока смещения. Это позволило ему завершить созданную им теорию электромагнитного поля, которая позволила не только объяснить электрические и магнитные явления, но и предсказать новые, существование которых было впоследствии подтверждено.

В основе теории Максвелла лежат четыре уравнения.

1. Электрическое поле может быть как потенциальным (EQ), так и вихревым (EB), поэтому напряженность суммарного поля E = EQ + EB.

Так как циркуляция вектора EQ равна нулю

           
а циркуляция вектора EB определяется выражением

           
то циркуляция вектора напряженности суммарного поля

[1]

Это уравнение показывает, что источниками электрического поля могут быть не только электрические заряды, но и изменяющиеся во времени магнитные поля.

2. Обобщенная теорема о циркуляции вектора H

           

Это уравнение показывает, что магнитные поля могут возбуждаться либо движущимися зарядами (электрическими токами), либо переменными электрическими полями.

3. Теорема Гаусса для поля D
           
Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плотностью ρ, то формула [3] запишется в виде
            

4. Теорема Гаусса для поля B
            

Величины, входящие в уравнения Максвелла, не являются независимыми и между ними существует следующая связь (изотропные несегнетоэлектрические и неферромагнитные среды):
 
           

где ε0 и μ0 – соответственно электрическая и магнитная постоянная, ε и μ – соответственно диэлектрическая и магнитная проницаемость, γ – удельная проводимость вещества.

Из уравнений Максвелла вытекает, что источниками электрического поля могут быть либо электрические заряды, либо изменяющиеся во времени магнитные поля, а магнитные поля могут возбуждаться либо движущимися электрическими зарядами (электрическими токами), либо переменными электрическими полями.

Уравнения Максвелла не симметричны относительно электрического и магнитного полей. Это связано с тем, что в природе существуют электрические заряды, но нет зарядов магнитных. Для стационарных полей (E=const и B=const) уравнения Максвелла примут вид:

т.е. источниками электрического поля в данном случае являются только электрические заряды, источниками магнитного – только токи проводимости. В данном случае электрические и магнитные поля независимы друг от друга, что и позволяет изучать отдельно постоянные электрические и магнитные поля.
Воспользовавшись известными из векторного анализа теоремами Стокса и Гаусса

можно представить полную систему уравнений Максвелла в дифференциальной форме (характеризующих поле в каждой точке пространства):

Если заряды и токи распределены в пространстве непрерывно, то обе формы уравнений Максвелла – интегральная и дифференциальная – эквивалентны. Однако если имеются поверхности разрыва (поверхности, на которых свойства среды или полей меняются скачкообразно), то интегральная форма уравнений является более общей.

Уравнения Максвелла в дифференциальной форме предполагают, что все величины в пространстве и времени изменяются непрерывно. Чтобы достичь математической эквивалентности обеих форм уравнений Максвелла, дифференциальную форму дополняю граничными условиями, которым должно удовлетворять электромагнитное поле на границе раздела двух сред. Интегральная форма уравнений Максвелла содержит эти условия

Первое и последнее уравнение отвечают случаям, когда на границе раздела двух сред нет ни свободных зарядов, ни токов проводимости.

Уравнения Максвелла – наиболее общие уравнения для электрических и магнитных полей в покоящихся средах. Они играют в учении об электромагнетизме такую же роль, как законы Ньютона в механике. Из уравнений Максвелла следует, что переменное магнитное поле всегда связано с порождаемым им электрическим полем, а переменное электрическое поле всегда связано с порождаемым им магнитным, т.е. электрическое и магнитное поля неразрывно связаны друг с другом – они образуют единое электромагнитное поле.