 Принципы действия устройств
Принципы действия устройств  Полупроводники
ПолупроводникиПоиск по тегам : Полупроводники, p-n переход, примесные полупроводники, проводимость полупроводников, ВАХ
Каталог статей  Принципы действия устройств Принципы действия устройств  Полупроводники ПолупроводникиПоиск по тегам : Полупроводники, p-n переход, примесные полупроводники, проводимость полупроводников, ВАХ |
| Полупроводники. Принцип действия. Свойства электронно-дырочных переходов. |
|
СТРУКТУРА И ЭНЕРГЕТИЧЕСКИЕ ЗОНЫ ПОЛУПРОВОДНИКОВ В абсолютном большинстве случаев устройства современной электроники изготавливаются из полупроводниковых материалов. Полупроводниками обычно называют материалы, удельное сопротивление которых больше, чем у проводников (металлов), но меньше, чем у изоляторов (диэлектриков). Сразу следует заметить, что различие между полупроводниками и диэлектриками только количественное, тогда как различие между полупроводниками и металлами более принципиальное - качественное. Полупроводники являются разновидностью диэлектриков, можно сказать, что они являются диэлектриками с уменьшенным удельным сопротивлением, тогда как с металлами у них значительно меньше общего. Для того чтобы представить особенности полупроводниковых материалов, следует рассмотреть их структуру и энергетические зоны. Любое твердое тело представляет собой множество атомов, сильно взаимодействующих друг с другом благодаря малым межатомным расстояниям. Эти расстояния минимальны у металлов и максимальны у диэлектриков. Однако в любом случае всю совокупность атомов в куске твердого тела следует рассматривать как единую целую структуру, которая подобно атому характеризуется некоторым единым энергетическим спектром. Особенность этого спектра в том, что он состоит из дискретных разрешенных зон. Строго говоря, разрешенные зоны сами имеют дискретную структуру и состоят из большого числа разрешенных уровней (равного числу атомов в рассматриваемом образце), неэнергетические расстояния между ними малы (~10-22эВ), поэтому иногда разрешенные зоны можно считать сплошными. На рис. 1.1 приведена зонная диаграмма для полупроводника. Прежде всего, следует обратить внимание на запрещенную зону (зону запрещенных энергий), которая разделяет разрешенные зоны. Отметим, что у диэлектриков ширина запрещенной зоны больше, чем у полупроводников, а у металлов разрешенные зоны сливаются, так что заращенной зоны у них нет. Ширина запрещенной зоны εз, определяющая энергетический промежуток запрещенных энергий, является важнейшим параметром полупроводника. Для наиболее часто используемых в электронике полупроводников германия, кремния и арсенида галлия - ширина запрещенной зоны равна соответственно 0,7; 1,1 и 1,4 эВ.
Верхняя разрешенная зона называется зоной проводимости. Электроны, находящиеся в этой зоне, обладают довольно большой энергией и могут ее изменять под действием электрического поля, перемещаясь в объеме полупроводника. Электропроводность полупроводника и определяется этими электронами. Нижняя разрешенная зона называется валентной зоной. Энергетические уровни этой зоны обычно заполнены электронами внешней оболочки атомов - внешних устойчивых орбит (валентными электронами). При наличии свободных уровней в валентной зоне электроны также могут изменять свою энергию под действием электрического поля. Если же все уровни зоны заполнены, то валентные электроны не смогут принять участие в проявлении электропроводности полупроводника. Рассмотрим теперь структуру собственного (беспримесного) полупроводника. Монокристаллические полупроводники представляют собой кристаллы с регулярной структурой. Кристаллическая решетка кремния (германия) называется тетраэдрической или решеткой типа алмаза. Она характерна для всех четырехвалентных элементов. Для определенности будем рассматривать структуру кремния. Это справедливо хотя бы потому, что приблизительно 97% всех изделий полупроводниковой электроники на сегодняшний день выполняются на основе кремния. Связь атомов в кремнии устанавливается вследствие наличия специфических обменных сил, возникающих при парном объединении валентных электронов. У соседних атомов кремния появляются общие отбиты, на которых в соответствии с фундаментальным положение физики, называемым принципом запрета Паули, находится не более двух электронов. Поскольку атом кремния имеет четыре валентных электрона, то он использует эти электроны для связи с четырьмя другими атомами, которые, в свою очередь, также выделяют по одному валентному электрону для связи с каждым из своих четырех соседних атомов. Таким образом, получается, что любой атом кремния связан с каждым из четырех соседних атомов общей орбитой, причем на этой общей орбите находится два электрона. Такая связь атомов называется парно-электронной или ковалентной. На рис. 1.2 приведена упрощенная модель решетки (а) и зонная энергетическая диаграмма (б) для беспримесного кремния. На этом рисунке между каждыми двумя атомами кремния проведены две связывающие их прямые линии. Каждая такая линия символизирует собой наличие электрона на общей орбите у этих атомов. Ее принято называть связью (валентной связью). Валентный электрон, находящийся в такой связи, по энергии расположен в валентной зоне.
Электроны во всех связях будут присутствовать только при температуре абсолютного нуля. По мере нагревания полупроводника происходит нарушение связей, т.е. некоторые валентные электроны получают от тепла энергию, необходимую для их перехода в зону проводимости (рис. 1.2, б). Такой переход соответствует ионизации связи и выходу из нее электрона (рис. 1.2, а). Появившиеся свободные электроны будут принимать участие в образовании тока в полупроводнике (при приложении напряжения к полупроводнику). Появление вакантных уровней в валентной зоне свидетельствует о том, что для валентных электронов появляется возможность изменять свою энергию (появляется возможность переходить с одного разрешенного уровня валентной зоны да другой), а следовательно, участвовать в процессе протекания тока через полупроводник. С повышением температуры возрастает число свободных электронов в зоне проводимости и число вакантных уровней в валентной зоне. Заметим, что этот процесс будет проходить интенсивнее в полупроводниках с узкой запрещенной зоной. Вакантный энергетический уровень в валентной зоне и соответственно ионизированную валентную связь принято называть дыркой. Дырка является подвижным носителем положительного заряда, равного по модулю заряду электрона. Перемещение дырки (положительного заряда) соответствует встречному перемещению валентного электрона (из связи в связь). Движение дырки есть поочередная ионизация валентных связей. Отметим, что процесс образования свободного электрона и дырки принято называть генерацией. Поскольку в рассматриваемом случае генерация происходит под действием тепла, то ее можно назвать термогенерацией. Появление электрона в зоне проводимости и дырки в валентной зоне на энергетической диаграмме (см. рис. 1.2, б) представлено в виде кружочков с соответствующими знаками зарядов. Стрелкой обозначен переход электрона из валентной зоны в зону проводимости. Таким образом, за счет термогенерации в собственном (беспримесном) полупроводнике, который принято обозначать буквой i, образуются два типа подвижных носителей заряда: свободные электроны n и дырки p, причем их число одинаково (ni = pi). Эти носители заряда иногда называют собственными, а электропроводность, ими обусловленную, - собственной электропроводностью. В полупроводниковой электронике, в отличие от собственной электропроводности, наиболее части используют примесную электропроводность, характерную для примесных полупроводников.
Примесными полупроводниками принято называть полупроводники, электропроводность которых обусловлена носителями заряда, образующимися при ионизации атомов. Если в кремний ввести атом пятивалентного элемента (например, фосфора), то четыре из пяти валентных электронов этого элемента вступят в связь с четырьмя соседними атомами кремния (подобно атомам собственного полупроводника). Пятый е электрон будет в данном случае избыточным. Он оказывается очень слабо связанным со своим атомом, поэтому оторвать его от атома и превратить в свободный носитель заряда можно даже оторвать его от атома и превратить в свободный носитель заряда можно даже при воздействии малой тепловой энергии. На энергетической диаграмме, соответствующей рассматриваемому случаю (рис. 1.3), обозначен разрешенный энергетический уровень εд, который принес с собой атом фосфора. На этом уровне при очень низкой температуре и будет находиться избыточный электрон фосфора. При незначительном повышении температуры он переходит в зону проводимости и становится свободным. Нейтральный атом фосфора при этом превращается в положительный ион (его заряд обусловлен отсутствием валентного электрона). Количество энергии, необходимое для отделения избыточного электрона и образования иона, называется энергией активации (ионизации) примеси (∆εА ≈ 0,1 эВ). Отметим, что ион прочно связан с кристаллической решеткой и не может перемещаться подобно дырке. Таким образом, появление в кремнии атома фосфора привело к образованию в зоне проводимости свободного электрона. Образование данного электрона не связано с существованием дырки. В реальных случаях вводится, конечно, далеко не единственный атом примеси (1014...1018 атомов / см3), поэтому и примесных уровней получается довольно много. Примесные уровни образуют примесную зону, которая в рассматриваемом здесь случае будет находиться в запрещенной зоне кремния вблизи зоны проводимости.
Атомы пятивалентной примеси принято называть донорами. Примесные разрешенные уровни, приносимые донорами, называют донорными. Примесные полупроводники, полученные за счет введения доноров, называются электронными, или полупроводниками n-типа. Электропроводность электронных полупроводников определяется свободными электронами, которые здесь являются основными носителями заряда. Дырки в полупроводнике n-типа являются неосновными носителями заряда. Дырок здесь очень мало (nn ›› рn), но они все-таки есть (дырки образуются за счет термогенерации подобно собственным носителям в беспримесном полупроводнике). Итак, за счет введения донорной примеси образуется электронный полупроводник, электропроводность которого определяется электронами, причем число свободных электронов практически равно числу ионизированных доноров. Рассмотрим теперь дырочный полупроводник или полупроводник р-типа. Такой полупроводник получается за счет введения в него трехвалентных атомов примеси (например, бора). Атомы трехвалентной примеси принято называть акцепторами. Находясь среди атомов кремния, атом бора образует только три заполненные валентные связи. Четвертая связь оказывается незаполненной, однако она не несет заряда, т. е. атом бора является электрически нейтральным. При воздействии даже небольшой тепловой энергии электрон одной из соседних заполненных валентных связей кремния может перейти в эту связь. Во внешней оболочке атома бора появляется лишний электрон, т. е. атом бора превращается в отрицательный ион. Ионизированная связь атома кремния (из которой электрон перешел к атому бора) несет собой уже положительный заряд, являясь дыркой. На энергетической диаграмме, соответствующей рассматриваемому здесь случаю (рис. 1.4), обозначен разрешенный энергетический (акцепторный) уровень εА, который принес с собой атом бора. Этот уровень будет не заполнен лишь при очень низкой температуре. При небольшом повышении температуры один из электронов валентной зоны переходит на акцепторный уровень, затратив при этом небольшую энергию, равную энергии активации примеси (∆εА ›› 0,1эВ). Таким образом, получаются дырка (в валентной зоне) и ионизированный акцептор.
Электропроводность дырочного полупроводника определяется дырками, которые здесь являются основными носителями заряда. Электроны в полупроводнике р-типа являются неосновными носителями и их очень мало (рр ›› np).Итак, за счет введения и активации акцепторной примеси образуется дырочный полупроводник, электропроводность которого определяется дырками, причем число и практически равно числу ионизированных акцепторов. При рассмотрении примесных полупроводников обычно используют понятие «концентрация примеси». Концентрацией называется число зарядов или частиц в единичном объеме (например, в 1 см3). Понятно, что чем больше концентрация доноров Nд, тем больше и концентрация электронов, а чем больше концентрация акцепторов NА, тем больше концентрация дырок в полупроводнике. Если оба типа примеси находятся в равном количестве (Nд = NА) принято называть компенсированным. Компенсированный проводник похож на собственный (nk = pk), но имеет ряд интересных свойств и отличий. Необходимо отметить, что рассмотренные выше процессы являются, вообще говоря, обратимыми. Наряду с переходами электронов с нижних энергетических уровней на более высокие происходят и обратные переходы. Особое внимание обратим на то, что одновременно с генерацией пар «электрон-дырка» происходит и обратный процесс - процесс взаимного уничтожения свободного электрона и дырки, который принято называть рекомбинацией (свободный электрон переходит из зоны проводимости в валентную зону). При некоторой установившейся температуре полупроводник находится в состоянии термодинамического равновесия. Процесс генерации уравновешивается процессом рекомбинации. Одним и основных параметров полупроводника является уровень Ферми, вероятность заполнения которого при температуре, отличной от абсолютного нуля, равна 0,5. Энергетический уровень Ферми представляет собой среднюю термодинамическую энергию тела на один электрон. Фундаментальное положение физики указывает, что уровень Ферми одинаков во всех частях равновесной системы, какой бы разнородной она ни была. Для собственных полупроводников уровень Ферми проходит по середине запрещенной зоны. В электронном полупроводнике в сравнении с собственным имеется большое число электронов в зоне проводимости, т.е. средняя энергия электронов (и всего полупроводника) здесь будет выше. Следовательно, в электронном полупроводнике уровень Ферми должен находиться выше середины запрещенной зоны, причем, чем больше концентрация доноров, тем выше будет располагаться уровень Ферми. Аналогично можно заключить, что в дырочном полупроводнике уровень Ферми должен быть ниже середины запрещенной зоны, причем тем ниже, чем больше концентрация акцепторов. Необходимо отметить, что помимо рассмотренных здесь примесных полупроводников в электронике находят применение и так называемые вырожденные полупроводники. У таких полупроводников уровень Ферми обычно располагается в разрешенных зонах: в озоне проводимости для электронного и в валентной зоне для дырочного полупроводника. На практике обычно используются вырожденные полупроводники с сильной степенью вырождения (например, в туннельных диодах), получаемые за счет значительного повышения концентрации примеси (1019 ...1021 см -3).
Выше были ниже рассмотрены некоторые параметры полупроводников, в то числе и самый важный - ширина запрещенной зоны. В этом разделе остановимся на параметрах, в той или иной степени влияющих на электропроводность полупроводника. Эти параметры часто используются при описании принципа действия и характеристик многих элементов полупроводниковой электроники. Вторым по значимости параметром полупроводника (после εз), пожалуй, является подвижность носителей заряда μ. Подвижность носителей по определению есть их средняя направленная скорость в полупроводнике при напряженности электрического поля Е = 1 В / см. Как правило, подвижность электронов μn всегда больше подвижности дырок μр. Это объясняется большей инерционностью дырок (соответствующей инерционности валентного электрона), чем свободного электрона. Наиболее значительно это проявляется у арсенида галлия. Чем больше подвижность, тем больше скорость движения носителей и тем выше быстродействие полупроводникового элемента. Отсюда становится понятным преимущество высокочастотных элементов, изготовленных из электронного арсенида галлия. Подвижность носителей заряда зависит от ряда факторов, важнейшим из которых является температура. Зависимость μ от температуры определяется механизмом рассеяния носителей. Поскольку с повышением температуры увеличивается интенсивность колебания атомов кристаллической решетки, то возрастает и число столкновений в единицу времени, следовательно, наблюдается падение подвижности носителей. Для кремния п-типа можно записать
где μ0 - подвижность носителей при начальной (комнатной) температуре Т0. Аналогичные зависимости имеют место и для других полупроводниковых материалов; отличие заключается только в величинах показателя степени. Подвижность носителей заряда в примесных полупроводниках обычно уменьшается с повышением концентрации примесей, причем степень влияния концентрации примесей на возрастает при ее увеличении. При очень больших напряженностях электрического поля (больших значениях критической напряженности Екр) подвижность уменьшается по закону
Здесь μ0 - подвижность носителей заряда при Е = Екр (для кремния n-типа, например, Екр= 2,5 кВ / см). Подвижность носителей заряда связана с другим параметром полупроводника - коэффициентом диффузии D-соотношением, которое принято называть соотношением Эйнштейна: D = φтμ, где φт = kТ / q - тепловой потенциал, который при комнатной температуре приближенно равен 26 мВ; k - постоянная Больцмана; q - заряд электрона. Коэффициенты D, так же как и подвижности, имеют разные значения для электронов и дырок, причем Dn > Dp. Еще одним важным параметром полупроводника является время жизни τ. Различают непосредственную рекомбинацию и рекомбинацию через ловушки. Непосредственной рекомбинацией называют переход электрона из зоны проводимости непосредственно в валентную зону, где он занимает вакантный уровень и уничтожает дырку. В некоторых элементах, выполненных на основе арсенида галлия и некоторых других полупроводников, непосредственная рекомбинация может играть важную роль. Однако в таких полупроводниках, как германий и кремний, непосредственная рекомбинация маловероятна. В большинстве практических случаев главную роль играет рекомбинация через ловушки (рис. 1.5). Ловушками называются глубокие энергетические уровни, расположенные вблизи середины запрещенной зоны. Ловушки образуются за счет введения особых примесей или наличия дефектов кристаллической решетки полупроводника. Реально всегда существуют и мелкие дефектные уровни (уровни прилипания), которые расположены вблизи дна или потолка запрещенной зоны, но на процесс рекомбинации они практически не влияют. Рекомбинация через ловушки происходит в два этапа: сначала электрон переходит из зоны проводимости на уровень ловушки, а затем с уровня ловушки в валентную зону. Эти переходы обозначены стрелками на рис. 1.5.
Чем больше в полупроводнике ловушек, тем интенсивнее происходит рекомбинация и соответственно меньше τ. Поэтому малые времена жизни свойственны полкристалла, где дефекты расположены на всех гранях отдельных зерен, и поверхностным слоям монокристаллических полупроводников, где много различных дефектов и посторонних примесей. В общем случае движение носителей заряда в полупроводниках обусловлено двумя физическими процессами: диффузией и дрейфом. Диффузией называется направленное перемещение носителей зарядов в следствие неравномерности их концентрации, т.е. перемещение под действием градиента концентрации носителей зарядов. Дрейфом называется направленное перемещение носителей заряда под действием электрического поля. За время жизни в результате диффузионного движения носители заряда будут проходить некоторое среднее расстояние L, называемое диффузионной длиной. Более строго диффузионная длина определяется как расстояние, на котором концентрация носителей уменьшится в е (~ 2,7) раз. Диффузионную длину можно определить как L = √DƮ. С точки зрения конструирования и эксплуатации элементов полупроводниковой электроники очень важным параметром является удельная проводимость полупроводников.
Поскольку в полупроводниках имеется два типа подвижных носителей заряда, удельная проводимость σ складывается из двух составляющих: электронной и дырочной, т. е. σ = qnμn + qpμp. Поскольку для собственного полупроводника обе составляющие равнозначны, можно записать: σi = qni (μn + μp). Отметим, что концентрация носителей заряда в собственном полупроводнике при заданной температуре определяется шириной запрещенной зоны. Так, поскольку εз, у германия меньше, чем у кремния, ni, у германия больше (приблизительно на три порядка), чем у кремния. Аналогично для электронного полупроводника запишем:
Формула (1.3) является общей для любого состояния полупроводника n-типа. Если донорная примесь активировалась, то n можно заменить на пп. Удельная проводимость дырочного полупроводника определяется как
Сравнение (1.3) и (1.4) позволяет сделать важный практический вывод: при равной концентрации примесей электронный полупроводник будет иметь большую удельную проводимость, чем дырочный, поскольку μn > μp. Рассмотрим теперь температурную зависимость проводимости полупроводника, например электронного. Так как при температуре абсолютного нуля в полупроводнике отсутствуют свободные носители заряда, то n = 0, следовательно, σn = 0. При повышении температуры σn будет увеличиваться за счет активации примесных атомов (доноров). В этом случае электроны с донорных уровней (донорной зоны) переходят в зону проводимости (см. рис.1.3), что соответствует возрастанию n в формуле (1.3). Этот рост будет происходить до тех пор, пока не активируется вся примесь. Температура, при которой все атомы примеси уже отдали свои избыточные валентные электроны, принято называть температурой активации tакт. Эта температура определяется типом примеси и ее концентрацией. В первом приближении можно считать tакт = -100 ˚С. Поскольку вся примесь уже активирована, то при дальнейшем повышении температуры концентрация электронов остается практически постоянной. Это соответствует qn = const в формуле (1.3). Следовательно, теперь изменение проводимости будет определяться лишь изменением подвижности носителей, т.е. σn будет изменяться по закону (1.1). При дальнейшем повышении температуры проводимость резко возрастает за счет интенсивной термогенерации. Здесь температура становится уже достаточной для перевода электронов из валентной зоны в зону проводимости. Поскольку сильно увеличивается как число электронов, так и число дырок (собственная электропроводность преобладает над примесной), то проводимость полупроводника резко возрастает. Температура tкр, начиная с которой происходит возрастание проводимости, называется критической, или температурой вырождения. Хотя tкр и зависит от концентрации примесных носителей, определяющим параметром для нее является ширина запрещенной зоны. Чем шире запрещенная зона, тем больше tкр. Так, если для кремния tкр ≈ 330 ˚С, то для германия критическая температура будет меньше (~ 100 ˚С). Рабочий температурный диапазон примесных полупроводников ограничен снизу tакт, а сверху - tкр. Абсолютное большинство полупроводниковых устройств электроники и используются в этом диапазоне температур (обычно даже в более узком диапазоне: - 60 ...100 ˚С). Таким образом, основной рабочей областью полупроводника является область, в которой его проводимость уменьшается с ростом температуры.
СТРУКТУРА И ОСНОВНЫЕ СВОЙСТВА р-n ПЕРЕХОДА Прежде всего, рассмотрим два образца полупроводника с электронной и дырочной электропроводностями (рис. 1.6, а). Напомним, что в дырочном полупроводнике присутствуют в равном количестве подвижные положительные дырки и неподвижные отрицательные ионы. На рис. 1.6,а дырки обозначены знаками «плюс», а отрицательные ионы - знаками «минус», заключенными в кружки. Для нашего рисунка концентрация примеси в электронном полупроводнике выбрана в 2 раза меньше, чем в дырочном. Аналогично обозначениям зарядов в дырочном полупроводнике в электронном полупроводнике электроны обозначены знаками «минус», а положительные ионы - со знаками «плюс», заключенными в кружки. Поскольку NA = 2NД, то заряды в дырочном полупроводнике нарисованы в 2 раза чаще, чем в электронном. Теперь представим, что рассмотренные нами два образца являются просто областями единого кристалла полупроводника (рис. 1.6, б). Тогда по закону диффузии электроны из области n будут перемещаться в область р, а дырки, наоборот, - из области р в область n. Встречаясь на границе р и п областей, дырки и электроны рекомбинируют. Следовательно, в этой пограничной области значительно уменьшается концентрация носителей заряда и обнажаются некомпенсированные заряды неподвижных ионов. Со стороны области обнажаются положительные заряды доноров, а со стороны области р-отрицательные заряды акцепторов. Область некомпенсированных неподвижных зарядов и есть собственно область р-п перехода. Ее часто называют обедненным, истощенным слоем, или i-областью, имея ввиду резко сниженную концентрацию подвижных носителей заряда. Иногда эту область называют запорным слоем электронно-дырочного перехода. 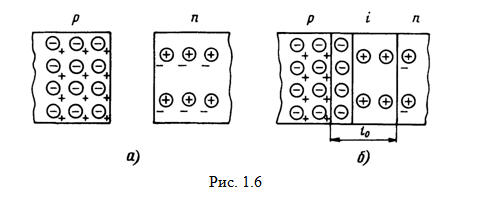 В реальных р-п переходах концентрации доноров и акцепторов отличаются на несколько порядков. В таких несимметричных переходах практически весь обедненный слой сосредоточен в слаболегированной части. Ширина обедненного слоя (i-области) в равновесном состоянии l0 (см. рис. 1.6, б) является важным параметром р-п перехода. Другим, не менее важным параметром равновесного состояния является высота потенциального барьера (контактная разность потенциалов) ∆φ0. Этот параметр показан на зонной энергетической диаграмме р-п перехода, изображенной на рис. 1.7 (где εF - уровень Ферми). Потенциальный барьер образуется электрическим полем пространственного заряда обедненного слоя. При отсутствии внешнего поля (равновесное состояние) уровень Ферми является общим для всего объема полупроводника и расположен в запрещенной зоне. Поскольку в полупроводнике п-типа уровень Ферми смещен вверх относительно середины запрещенной зоны, а в полупроводнике р-типа вниз, то разрешенные зоны дырочной области должны располагаться на более высоких энергиях, чем разрешенные зоны электронной энергии. Следовательно, в обедненном слое диаграмма энергетических зон искривляется. Заметим, что в i-области уровень Ферми проходит вблизи середины запрещенной зоны.
Электрическое поле электронно-дырочного перехода, представляемое на рис. 1.7 потенциальным барьером, препятствует прохождению электронов из области р-типа в область п-типа и дырок в обратном направлении. Более строго: дрейфовые составляющие тока равны диффузионным. С некоторым приближением можно считать, что в равновесном состоянии р-п перехода его внутреннее электрическое поле компенсирует процесс диффузии носителей заряда, в результате чего ток через р-п переход не протекает. Анализируя рис. 1.7, следует помнить, что электроны в зоне проводимости стремятся занять уровни минимальной энергии, а дырки в валентной зоне - максимальной энергии. Высоту потенциального барьера ∆φ0 удобно выражать в единицах напряжения - вольтах. Довольно сильное влияние на величину ∆φ0 оказывает ширина запрещенной зоны исходного полупроводника: чем больше εз, тем больше и ∆φ0. Так, для большинства р-п переходов из германия ∆φ0 = 0,35 В. а из кремния - 0,7 В. Ширина р-п перехода во многом определяется величиной ∆φ0. Это хорошо видно из общей формулы для l0 при Na ›› Nд:
где εo, εn - диэлектрическая проницаемость вакуума и полупроводника соответственно. Величина l0 обычно составляет десятые доли или единицы микрометра. Из (1.5) следует, что для создания широкого р-п перехода следует использовать малые концентрации примеси, а для создания узкого перехода - большие концентрации. При равных концентрациях примеси l0 будет больше у р-п перехода с большим ∆φ0 и, следовательно, с большей εз. Таким образом, у кремниевых р-п переходов l0 обычно больше, чем у германиевых. Если к р-п переходу подключить внешний источник напряжения, то нарушится условие равновесия и потечет ток. При этом должна измениться высота потенциального барьера и соответственно ширина р-п перехода. Рассмотрим сначала прямое смещение р-п перехода (рис. 1,8). В этом случае внешнее напряжение U приложено в прямом направлении, т. е. знаком «плюс» к области р-типа. Высота потенциального барьера ∆φ при этом снижается:
Уменьшение высоты потенциального барьера приводит к снижению электрического поля, препятствующего диффузии носителей заряда. Дырки из области р-типа начинают переходить в область n-типа, а электроны, наоборот, из области р-типа в область n-типа. В каждой области появляются избыточные концентрации неосновных носителей. Процесс нагнетания неосновных носителей заряда в какую-либо область полупроводника называется инжекцией. За счет разной концентрации примеси в областях несимметричных р-п переходов концентрации основных носителей тоже будут разные (обычно отличаются на несколько порядков). В рассматриваемом нами случае Na ›› Nд, следовательно, рр » рп. Сильнолегированную дырочную область обозначим как р+ (рис. 1.8). Она имеет относительно малое удельное сопротивление и обычно называется эмиттером. Область n-типа, имеющая относительно большое удельное сопротивление, называется базой. В несимметричных р-п переходах концентрация инжектированных носителей из эмиттера в базу всегда гораздо больше, чем в обратном направлении. Параметром, характеризующим степень однонаправленности инжекции, является коэффициент инжекции γ. Для рассматриваемого нами перехода можно записать
γ = Iр / (Iр + In),
где Ip, In - токи инжекции дырок и электронов соответственно. В реальных р-п переходах инжекция имеет практически односторонний характер: носители инжектируются в основном из эмиттера в базу (Iр ›› In), т. е. γ ≈ 1. Для практических расчетов удобно использовать формулу
где ρэ, ρб - удельные сопротивления эмиттера и базы соответственно. Из (1.7) следует, что чем сильнее легирован эмиттер и чем слабее легирована база, тем ближе значение у к единице. Теперь рассмотрим обратное смещение р-п перехода (рис. 1.9). В этом случае внешнее напряжение U приложено в обратном направлении, т. е. знаком «плюс» к области n-типа. Высота потенциального барьера ∆φ при этом повышается:
Подставляя значение ∆φ из (1.8) в формулу (1.5), получаем для неравновесной ширины р-п перехода l:
Таким образом, увеличение обратного смещения приводит к расширению р-п перехода. Поскольку несимметричный переход почти полностью расположен в высокоомной базе, то и его расширение происходит в сторону базы. При использовании обратного смещения р-п перехода на практике обычно U » ∆φ. В этом случае (1.9) можно переписать в виде
При приложении U в обратном направлении концентрации неосновных носителей на границах i-области уменьшаются по сравнению с равновесными значениями. Такой процесс отсоса носителей называется экстракцией.
В общем виде вольт-амперная характеристика (ВАХ) р-n перехода (рис. 1.10) представляется экспоненциальной зависимостью
где I0 - обратный ток. Этот ток имеет небольшие величины (мкА или нА), но довольно сильно увеличивается при повышении температуры. Подробно I0 рассмотрим далее.
Из (1.11) следует, что при прямом смещении (U > 0) ток через р-п переход возрастает, а при обратном смещении (U < 0) становится малым, приближаясь к значению I0. Поскольку φТ = 26 мВ, то при положительных напряжениях U > 0,1В, в формуле (1.11) можно пренебречь единицей по сравнению с экспонентой. Таким образом, р-п переход характеризуется свойством односторонней электропроводности, т. е. хорошо проводит ток в прямом направлении и плохо в обратном. Следовательно, р-п переход обладает выпрямляющим действием, что позволяет использовать его в качестве выпрямителя переменного тока. Важным параметром р-п перехода является его дифференциальное сопротивление rд. Формулу для определения rд прямой ветви ВАХ получим из (1.11):
При I ›› I0 получим окончательно:
C ростом тока дифференциальное сопротивление р-п перехода быстро падает. При токах порядка единиц и десятков миллиампер rД составляет десятки и единицы Oм. При расчете выпрямительных устройств часто пользуются другим параметром р-п перехода - сопротивлением постоянному току Rст. Из формулы (1.11) довольно просто получить зависимость Rст от рабочего тока:
При прямом смещении р-п перехода (при протекании прямого тока) Rст всегда больше сопротивления rд. Поскольку на р-п переходе при больших токах может выделяться достаточно большая мощность, температура перехода при этом может заметно превысить температуру отдельных областей полупроводникового элемента и окружающей среды. Тепловой баланс в полупроводниковой структуре устанавливается через некоторое время после включения тока и определяется теплопроводностью отдельных частей структуры. С целью повышения максимально допустимой мощности, выделяемой на р-п переходе, прежде всего следует улучшить теплообмен с окружающей средой. Более подробно вопрос теплового режима будет рассмотрен в гл. 3. При прямом смещении р-п перехода его идеализированная ВАХ согласно (1.11) представляется однородной экспонентой. Однако реальная характеристика имеет несколько более сложную форму: состоит из нескольких участков с разными наклонами. Отличия реальной ВАХ от идеализированной определяются несколькими причинами. Первая причина обусловлена процессами рекомбинации в i-области р-п перехода. Она имеет место при малых прямых смещениях. В этом случае ∆φ еще велика, следовательно, имеет место малый уровень инжекции, т. е. в i-область из эмиттера и базы попадает малое число носителей заряда. При таком малом положительном смещении ширина перехода l еще довольно большая - объем i-области еще достаточно велик, следовательно, в ней присутствует относительно много ловушек. Таким образом, за счет большого числа ловушек создаются очень благоприятные условия в i-области для рекомбинации малого числа инжектированных носителей. В рассмотренном случае ВАХ формируется за счет тока рекомбинации, который тоже имеет экспоненциальную зависимость от напряжения, но более пологую, чем по (1.11). За счет такого пологого начального участка вид прямой ветви реальной ВАХ становится таким, как показано на рис. 1.11. На этом рисунке представлен параметр UП, называемый напряжением «пятки». Хотя на сегодняшний день и нет четкого определения для этого параметра, он часто используется для прикидочных расчетов радиоэлектронных устройств. Будем несколько условно считать, что UП - это напряжение на р-п переходе, при котором I = 0,1 мА. Нетрудно заметить, что чем больше ∆φ0 и l0 (чем шире ε3), тем должно быть больше и UП. Следовательно, у кремниевых р-п переходов UП больше, чем у германиевых, и меньше, чем у переходов из арсенида галлия (рис. 1.11). Следует отметить, что в формирование величины UП определенный вклад вносит и ток I0.
Другая причина отличия реальной ВАХ от формы (1.11) обусловлена падением напряжения на объемном сопротивлении базы. Эта причина проявляется при достаточно больших токах. Заметим, что сопротивление базы rб в реальных р-п переходах обычно составляет единицы или десятки Ом. Падение напряжения на этом сопротивлении Irб является той поправкой, которую следует ввести в формулу (1.11), чтобы учесть различие между напряжением на самом запорном слое р-п перехода и величиной внешнего напряжения U. С учетом такой поправки получаем
Падение напряжения на rб приводит к появлению на ВАХ участка, называемого омическим. При больших токах значение ∆φ0 становится небольшим, сопротивление обедненного слоя уменьшается и уже оказывается малосущественным, следовательно, в таком случае можно рассматривать р-п переход как простую двухслойную пластину, сопротивление которой приближенно равно сопротивлению ее высокоомного слоя rб (ρэ«ρб). Необходимо отметить, что учитывать падение напряжения на rб необходимо для значительного, иногда даже основного, рабочего участка ВАХ р-п перехода. Еще одна причина отличия реальной ВАХ от идеализированной обусловлена модуляцией сопротивления базы при больших уровнях инжекции. Протекание больших токов определяется инжекцией большого числа носителей заряда из эмиттера в базу. В результате присутствия в базе большого числа неосновных носителей заряда ее объемное сопротивление уменьшится. Это обстоятельство делает необходимым учет влияния rб = f(I) в формуле (1.13) для больших уровней инжекции. Обратная ветвь ВАХ р-п перехода определяется обратным током, который, как отмечалось выше, обычно довольно сильно возрастает при повышении температуры. Не останавливаясь здесь на анализе обратной ветви, рассмотрим влияние температуры на прямую ветвь ВАХ р-п перехода. Температурная зависимость прямой ветви ВАХ согласно (1.11) определяется изменениями I0 и φт . Заметим, что при больших токах необходимо согласно (1.13) также учитывать изменение rб. Влияние этих температурно-зависимых параметров на ВАХ приводит к тому, что при малых прямых напряжениях ток возрастает с повышением температуры, а при больших - уменьшается. В принципе существует даже точка (область), где величина тока практически не зависит от температуры. Однако эта термостабильная точка редко используется на практике, поскольку имеет место при достаточно больших уровнях инжекции. Для большинства же реальных устройств ток в р-п переходе несколько возрастает с повышением температуры (при постоянном напряжении). На практике чаще всего принято оценивать влияние температуры на ВАХ р-п перехода, определяя изменение напряжения при постоянном токе. Для оценки изменения прямого напряжения при изменении температуры вводится температурный коэффициент напряжения (ТКН), характеризующий сдвиг ВАХ по оси напряжений. Обычно ТКН имеет отрицательный знак, что знаменует собой уменьшение напряжения на р-п переходе при постоянном токе с ростом температуры. Отметим, что ТКН зависит от тока и несколько уменьшается с его ростом. Для р-п переходов из кремния ТКН достигает - 3 мВ/град.
ЕМКОСТИ р-n ПЕРЕХОДА Инерционность р-п перехода во многом определяется его емкостями. Обычно выделяют две основные емкости р-п перехода: диффузионную и барьерную. При прямом смещении р-п перехода из эмиттера в базу инжектируются неосновные для базы носители заряда. Изменение прямого напряжения на р-п переходе приводит к изменению концентрации этих неравновесных неосновных носителей в базе, т. е. к изменению заряда в ней Qз. Изменение же заряда, вызванное изменением напряжения, можно рассматривать как действие некоторой емкости. Эта емкость называется диффузионной, поскольку неосновные носители заряда попали в базу за счет диффузии из эмиттера. На практике обычно используется дифференциальная диффузионная емкость Сд
Из (1.14) следует, что диффузионная емкость будет тем больше, чем больше ток через р-п переход и чем больше время жизни неосновных носителей в базе τ. Емкость Сд во многом определяет быстродействие элементов полупроводниковой электроники. При обратном смещении инерционность р-п перехода характеризуется емкостью, которая называется барьерной (или зарядной). Барьерная емкость Q определяется изменением пространственного заряда в i-области под действием приложенного напряжения. Ширина р-п перехода зависит от U по закону (1.10). При изменении l меняется и число нескомпенсированных ионов в i-области, т. е. меняется ее заряд. По этому р-п переход можно рассматривать как систему из двух проводящих плоскостей, разделенных диэлектриком, т. е. как плоский конденсатор. Величину барьерной емкости можно рассчитать по формуле плоского конденсатора: С = ε0εПSi / l Здесь Si - площадь р-п перехода. Подставляя в эту формулу (1.10), получаем
Как видно из (1.15), Сб зависит от величины приложенного напряжения, т. е. р-п переход может выполнять функции конденсатора переменной емкости. В заключение заметим, что, поскольку при прямом смещении р-п переход сужается, барьерная емкость растет. Однако в этом случае Сб оказывается менее существенной, чем Сд.
Как было отмечено выше, при обратном смещении р-п перехода в нем протекает лишь небольшой ток, называемый обратным. Этот ток I0 и формирует обратную ветвь ВАХ р-п перехода (см. рис. 1.10). В общем случае I0 состоит из четырех составляющих: теплового тока, тока термогенерации, тока утечки и канального тока. Тепловой ток обусловлен термогенерацией электронно-дырочных пар в областях р- и n-типа, удаленных от i-области не далее чем на диффузионную длину (рис. 1.12). Строго говоря, диффузионная длина для эмиттера и базы будет разной, но этот факт не играет принципиальной роли для качественного рассмотрения теплового тока. Электроны и дырки, возникающие в структуре, будут сортироваться электрическим полем: электроны устремляются в n-область, а дырки - в p-область. Следует отметить, что если термогенерации носителей заряда произошла в каком-либо месте структуры, удаленном от i-области более чем на L, то эти носители не смогут уже дойти до i-области - они раньше рекомбинируют и, естественно, не примут участия в образовании теплового тока.
Поскольку тепловой ток обусловлен процессами термогенерации носителей заряда, то он довольно сильно возрастает при увеличении температуры. Обычно тепловой ток возрастает в 2 раза при увеличении температуры на каждые 10°С. Естественной представляется зависимость теплового тока от ширины запрещенной зоны полупроводника, из которого выполнен р-п переход. Чем больше ε3, тем меньше вероятность термогенерации при заданной температуре и, следовательно, меньше тепловой ток. Относительно теплового тока остается заметить, что он является основной составляющей обратного тока у германиевых р-п переходов и слабо зависит от величины приложенного обратного напряжения. Другой составляющей обратного тока является ток термогенерации, который обусловлен генерацией носителей заряда в i-области под действием тепла. Этот ток отличается от теплового только местом, где образуются подвижные носители заряда. Величина тока термогенерации пропорциональна объему обедненного слоя, т. е. ширине р-п перехода. Он растет при увеличении l, т. е. пропорционален √U. Поскольку ток термогенерации, также как и тепловой ток образуется за счет термогенерации носителей заряда, то он, подобно тепловому, возрастает при увеличении температуры. Однако это возрастание происходит более интенсивно. Обычно ток термогенерации возрастает в 3 раза при увеличении температуры на каждые 10°С. В германиевых р-п переходах ток термогенерации пренебрежимо мал в сравнении с тепловым, а для переходов из кремния и арсенида галлия может стать заметной частью I0 при высоких температурах. Третьей составляющей обратного тока р-п перехода является ток утечки. Для р-п переходов, изготовленных из «достаточно широкозонных полупроводников, поверхностные утечки могут явиться основной составляющей, определяющей величину тока I0. Ток утечки обусловлен многими факторами: поверхностными энергетическими уровнями, молекулярными и ионными пленками, различными загрязнениями и т. д. При повышении напряжения ток утечки возрастает по линейному закону или еще более круто. Влияние же температуры на ток утечки выражено сравнительно слабо. Отметим, что характерной особенностью тока утечки является его временная нестабильность. Образование тока утечки, как правило, связано с несовершенством технологии изготовления. Примером р-п перехода, у которого ток утечки является основной составляющей обратного тока, является кремниевый переход, выполненный по сплавной технологии. Четвертой составляющей обратного тока р-п перехода является канальный ток. Он является основной составляющей для кремниевых р-п переходов, выполненных по планарной технологии. Не вдаваясь здесь в особенности планарной технологии отметим, что при ее использовании поверхность кремниевых р-п переходов покрывается защитной пленкой SiO2. Это покрытие, с одной стороны, практически устраняет ток поверхностной утечки, но, с другой стороны, порождает канальный ток. Канальный ток возникает за счет образования канала (очень тонкого слоя) n-типа в приповерхностной области р-типа, покрытой пленкой SiO2. Отметим, что канальный ток очень маленький: десятые доли или единицы наноампер. Заканчивая рассмотрение обратного тока отметим, что, хотя на его величину и влияют многие факторы, все же можно считать, что он возрастает при уменьшении ширины запрещенной зоны полупроводника, из которого выполнен р-п переход. Так, обратный ток в германиевых р-п переходах обычно на три - четыре порядка выше, чем в кремниевых.
Как отмечалось выше, при рабочих величинах обратных напряжений I0 невелик. Однако при превышении определенного уровня U обратный ток реального р-п перехода быстро увеличивается, т. е. наступает пробой. Под пробоем р-п перехода понимается явление резкого увеличения обратного тока при достижении обратным напряжением определенного критического значения. Все разновидности пробоя р-п перехода можно разделить на две основные группы пробоев: электрические и тепловые. Электрические пробои связаны с увеличением напряженности электрического поля в запорном слое р-п перехода, а тепловые - с увеличением рассеиваемой мощности и соответственно температуры. Рассмотрим, прежде всего, основные разновидности электрического пробоя: полевой (зенеровский), лавинный и поверхностный. Вид ВАХ электрического пробоя представлен на рис. 1.13. Основное внешнее отличие разновидностей электрического пробоя проявляется в величинах пробивного напряжения.
В узких р-п переходах при относительно небольших обратных напряжениях (U ≤ 7В) обычно возникает полевой пробой. В основе полевого пробоя могут лежать несколько эффектов. Так, под действием большой напряженности электрического поля становится возможной генерация носителей заряда энергиями меньше ε3. При малых пробивных напряжениях основным эффектом, определяющим развитие полевого пробоя, становится туннельный. Электрический пробой, возникающий под действием этого эффекта, часто называют туннельным. В относительно широких р-n переходах при обратных напряжениях больше 15 В возникает лавинный пробой, механизм которого заключается в лавинном размножении носителей заряда в сильном электрическом поле под действием ударной ионизации. Электрон и дырка в запорном слое р-п перехода, ускоренные электрическим полем на длине своего свободного пробега, могут при столкновении с решеткой кристалла разорвать валентную связь. В результате рождается новая пара «электрон-дырка» и процесс повторяется под действием этих новых носителей. Таким образом, сопротивление р-п перехода начинает падать, а ток резко возрастать. Для того чтобы носители заряда успели приобрести высокую скорость, необходимую при ударной ионизации, путь и время их разгона должны быть относительно велики. Поэтому лавинный пробой и наблюдается только в широких р-п переходах, т. е. переходах, использующих слаболегированные полупроводники. В области р-п перехода, выступающей на поверхность, обычно имеет место значительное изменение напряженности электрического поля. Поверхностный заряд может привести как к уменьшению, так и к увеличению l. В результате этого на поверхности р-п перехода происходит электрический пробой при напряжении, меньшем, чем в объеме. Это явление носит название поверхностного пробоя. Большую роль в возникновении поверхностного пробоя играют диэлектрические свойства поверхностных покрытий. В некоторых случаях раньше, чем возникнет электрический пробой, может произойти тепловой. В принципе существует несколько разновидностей и теплового пробоя - обычно различные локальные пробои. Однако основной интерес представляет тепловой пробой, возникающий за счет большого lо. Этот пробой возникает в тех случаях, когда не обеспечивается необходимый отвод тепла от р-п перехода. Чаще всего тепловой пробой возникает в мощных германиевых р-п переходах, поскольку в них протекает большой обратный ток. Поскольку lо велик, то даже при небольших обратных напряжениях (меньших напряжения электрического пробоя) выделяется большая мощность Р = UI0. Эта мощность нагревает р-п переход, что вызывает возрастание I0, который, в свою очередь, увеличивает Р. Такая взаимосвязь приводит к резкому увеличению тока, т. е. к пробою р-п перехода. На рис. 1.14 приведена типовая обратная ветвь ВАХ р-п перехода при тепловом пробое. Такая характеристика имеет участок с отрицательным дифференциальным сопротивлением. Начало этого участка соответствует температуре р-п перехода, близкой к tкр.
Заметим, что если I0 вырос благодаря электрическому пробою, то после этого может наступить тепловой пробой. Соответственно на ВАХ после вертикального пробойного участка, свойственного электрическому пробою, может иметь место участок с отрицательным сопротивлением. Необходимо подчеркнуть, что тепловой пробой является крайне нежелательным явлением, поскольку он приводит к выходу р-п перехода из строя. Поэтому в тех случаях, когда возможен тепловой пробой, необходимо последовательно с р-п переходом включать токоограничивающее сопротивление.
|
||||||||||||||||||||||||||||||||